Binary Tree Fundamentals

Notes

二叉树

1
2
3
4
5
class Node<T>{
    T val;
    Node left;
    Node right;
}

二叉树的遍历

144. 二叉树的前序遍历 - 力扣（LeetCode）
94. 二叉树的中序遍历 - 力扣（LeetCode）
145. 二叉树的后序遍历 - 力扣（LeetCode）

递归, 迭代, Morris -> 实现二叉树的先序、中序、后序遍历。

递归遍历

递归序。每次递归调用结束会返回到当前方法的调用处。

序是根节点在的位置。根的相对位置决定序。

  • 先序遍历：对于每一颗子树来说。都是根左右的顺序。
  • 中序遍历：左根右
  • 后序遍历：左右根

递归序。每次递归调用结束会返回到当前方法的调用处。
第一次进入节点root。第一次进入方法。
递归调用root.left。递归结束会回到原方法
递归调用root.right。递归结束会回到原方法

所以会三次进入当前调用方法的栈。

  • 先序遍历：就是在第一次进入方法的时候打印
  • 中序遍历：就是在第二次进入方法的时候打印
  • 后序遍历：就是在第三次进入方法的时候打印
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33

    // 递归方式遍历
    class TreeRecurTraversal{

        public void preorder(Node root){
            if(root == null) {
                return;
            }
            // println可以换成任意方法调用，来操作节点
            System.out.println(root.val);
            preOrder(root.left);
            preOrder(root.right);
        }

        public void inorder(Node root){
            if(root == null) {
                return;
            }
            inorder(root.left);
            System.out.println(root.val);
            inorder(root.right);
        }

        public void postorder(Node root){
            if(root == null) {
                return;
            }
            postorder(root.left);
            postorder(root.right);
            System.out.println(root.val);
        }

    }

迭代遍历

所有的递归都可以改写成非递归。
因为递归是程序语言在隐式地帮你压栈。

什么样的编程语言会不支持递归呢？ - 知乎
尾调用优化 - 阮一峰的网络日志
Java尾递归 - 掘金

Java在编译器层面没有优化尾递归调用
Why doesn’t Java have optimization for tail-recursion at all?
As explained by Brian Goetz (Java Language Architect at Oracle) in this video:
“in jdk classes […] there are a number of security sensitive methods that rely on counting stack frames between jdk library code and calling code to figure out who’s calling them.”

Anything that changed the number of frames on the stack would break this and would cause an error. He admits this was a stupid reason, and so the JDK developers have since replaced this mechanism.

He further then mentions that it’s not a priority, but that tail recursion will eventually get done.

N.B. This applies to HotSpot and the OpenJDK, other VMs may vary.

第 4 章: 柯里化（curry） · 函数式编程指北
functional programming - Does Java support Currying? - Stack Overflow

使用栈实现。
Stack，ArrayDeque，LinkedList的区别 - SegmentFault 思否
Java不要使用Stack，Deprecated。使用Deque。

  • 先序遍历
  1. 如果头不为空。初始化栈。压入栈。
  2. 如果栈不为空，
    1. 每次从栈中弹出一个节点cur。
    2. 打印(处理)cur
    3. 如果有右节点。push。如果有左节点push
  3. 当栈空时，处理结束
  • 中序遍历
  1. 如果头不为空。初始化栈。压入栈。
  2. 如果栈不为空，或者root不为null
    1. root不为空，push，把左边节点都push。
    2. 直到root为空。就开始弹出节点。每弹出一个节点就打印值。
    3. 然后去到右边节点。继续处理这个节点的左边界。
  3. 直到栈空了，并且root为null
    先左再头。再去到右树的先左再头。不断循环。
  • 后序遍历
  1. 如果头不为空 初始化两个栈，压入栈。
  2. 如果栈不为空，
    1. 每次从栈中弹出一个节点cur。
    2. push到另一个辅助栈
    3. 如果有左节点。push。如果有右节点push
  3. 依次弹出第二个栈中的元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
class TraversalOfBinaryTree{
    class TreeNode<T>{
        T val;
        TreeNode left;
        TreeNode right;

        TreeNode() {}
        TreeNode(T val){
            this.val = val;
        }
        TreeNode(T val, TreeNode left, TreeNode right) {
          this.val = val;
          this.left = left;
          this.right = right;
      }
    }

    public void preOrder(TreeNode root){
        if(root != null) {
            Stack<TreeNode> stack = new Stack();
            stack.push(root);
            while(!stack.isEmpty()){
                root = stack.pop();
                System.out.println(root.val)
                if(root.right != null){
                    stack.push(root.right);
                }
                if(root.left != null){
                    stack.push(root.left);
                }
            }
        }
    }

    public void inOrder(TreeNode root){
        if(root != null) {
            Stack<TreeNode> stack = new Stack();
            while(!stack.isEmpty() || root != null) {
                // 当左边遍历到根节点时，就开始处理右边节点的左子树
                if(root != null){
                    stack.push(root);
                    root = root.left;
                } else {
                    root = stack.pop();
                    System.out.println(root.val);
                    root = root.right;

                }
            }
        }

    }

    // TODO: Morris traversal
    public void postOrder(TreeNode root){
         if(root != null) {
            Stack<TreeNode> stack1 = new Stack();
            Stack<TreeNode> stack2 = new Stack();

            stack1.push(root);
            while(!stack1.isEmpty()){
                root = stack1.pop();
                stack2.push(root);
                if(root.left != null){
                    stack1.push(root.left);
                }
                if(root.right != null){
                    stack1.push(root.right);
                }
            }
            while(!stack2.isEmpty()) {
                System.out.println(stack2.pop().val)
            }
           
         }
    }
}

Morris Traversal

神级遍历——morris - 知乎

morris遍历是二叉树遍历算法的超强进阶算法，跟递归、非递归（栈实现）的空间复杂度，morris遍历可以将非递归遍历中的空间复杂度降为O(1)。从而实现时间复杂度为O(N)，而空间复杂度为O(1) 的精妙算法。

morris遍历利用的是树的叶节点左右孩子为空（树的大量空闲指针），实现空间开销的极限缩减。

线索二叉树 - 维基百科，自由的百科全书

记作当前节点为cur。

  1. 如果cur无左孩子，cur向右移动（cur=cur.right）
  2. 如果cur有左孩子，找到cur左子树上最右的节点，记为mostright
    1. 如果mostright的right指针指向null，让其指向cur，cur向左移动（cur=cur.left）
    2. 如果mostright的right指针指向cur，让其指向null，cur向右移动（cur=cur.right）
  3. cur为null时遍历结束

实现以上的原则，即实现了morris遍历。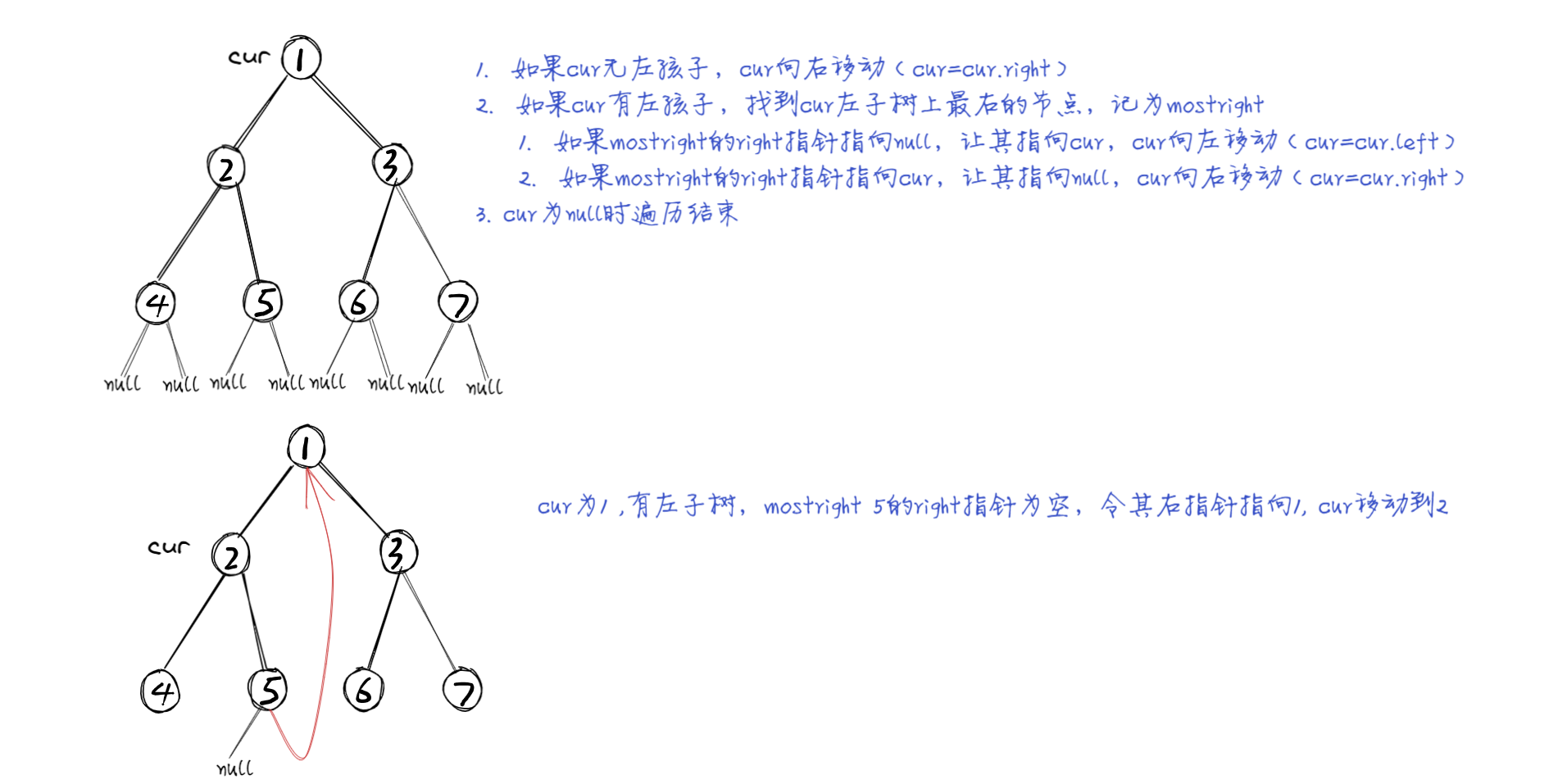

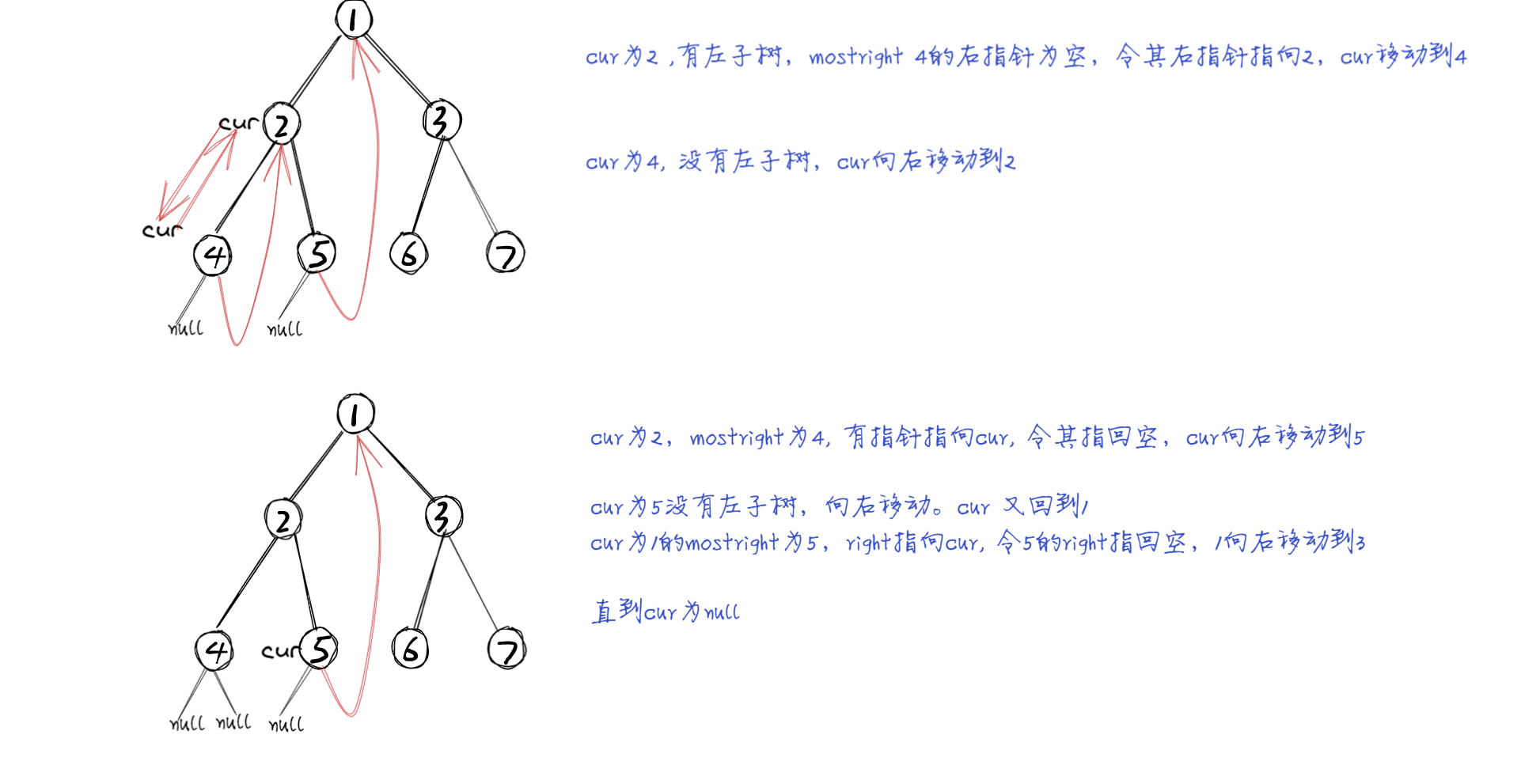
一个节点如果有左树，能够回到该节点两次。没有左树的节点只能到达一次。

如果左树上的mostright如果指向null，就是第一次来到当前节点。
如果左树上的mostright如果指向 cur，就是第二次来到当前节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class MorrisTraversal{
    public void morris(TreeNode root){
        if(root == null){
            return;
        }

        TreeNode cur = root;
        TreeNode mostRight;

        // cur为null时，遍历结束
        while(cur != null) {
            mostRight = cur.left;
            // 如果左子树为空，则跳过以下分支，直接向右移动
            if(mostRight != null){
                // 向右移动，找到most right。如果之前修改过这个mostright，则到第二个条件也要停止
                while(mostRight.right != null && mostRight.right!=cur){
                    mostRight = mostRight.right;
                }
                //  有指针指向空，则是第一次来到cur
                if(mostRight.right == null){
                    mostRight.right = cur;
                    cur = cur.left;
                    // 进行下一次while
                    //continue;
                }else{
                    mostRight.right =null;// 第二次来到cur
                    cur = cur.right;
                }
            } else{
                cur = cur.right;
            }
            //cur = cur.right;
        }
    }
}

时间复杂度：
遍历所有节点的mostright，最多是遍历两边，因此时间复杂度仍然是O(N)。

递归：

  • 先序遍历：就是在第一次进入方法的时候打印
  • 中序遍历：就是在第二次进入方法的时候打印
  • 后序遍历：就是在第三次进入方法的时候打印

Morris:
先序遍历：

  1. 如果一个节点只能到达一次，直接打印
  2. 如果一个节点能到达两次，第一次打印。

中序遍历：

  1. 如果一个节点只能到达一次，直接打印
  2. 如果一个节点能到达两次，第二次打印。

后序遍历：

  1. 只能到达一次的节点不打印
  2. 第二次到达节点，逆序打印左树的有边界mostright
  3. 所有节点遍历完之后，单独逆序打印整个树的右边界
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public static void morrisPre(Node head) {
    if(head == null){
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while (cur != null){
        // cur表示当前节点，mostRight表示cur的左孩子的最右节点
        mostRight = cur.left;
        if(mostRight != null){
            // cur有左孩子，找到cur左子树最右节点
            while (mostRight.right !=null && mostRight.right != cur){
                mostRight = mostRight.right;
            }
            // mostRight的右孩子指向空，让其指向cur，cur向左移动
            if(mostRight.right == null){
                mostRight.right = cur;
                System.out.println(cur.value);
                cur = cur.left;
                continue;
            }else {
                // mostRight的右孩子指向cur，让其指向空，cur向右移动
                mostRight.right = null;
            }
        }else {
            // 没有左树的节点，直接打印
            System.out.println(cur.value);
        }
        cur = cur.right;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public static void morrisIn(Node head) {
    if(head == null){
        return;
    }
    Node cur = head;
    Node mostRight = null;
    while (cur != null){
        mostRight = cur.left;
        if(mostRight != null){
            while (mostRight.right !=null && mostRight.right != cur){
                mostRight = mostRight.right;
            }
            if(mostRight.right == null){
                mostRight.right = cur;
                cur = cur.left;
                // 用continue能节省几行代码， 
                continue;
            }else {
                // 第二次来到该节点的时候打印
                mostRight.right = null;
            } 
        }
        // mostRight.right != null 和没有左子树的情况都要执行
        // 能回到两次的节点，当第二次量到达的时候，也就是mostRight.right != null时打印
        // 没有左树也会打印（只经过一遍的节点）
        System.out.print(cur.value);
        cur = cur.right;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
public static void morrisPost(Node head) {
       if(head == null){
           return;
       }
       Node cur = head;
       Node mostRight = null;
       while (cur != null){
           mostRight = cur.left;
           if(mostRight != null){
               while (mostRight.right !=null && mostRight.right != cur){
                   mostRight = mostRight.right;
               }
               if(mostRight.right == null){
                   mostRight.right = cur;
                   cur = cur.left;
                   continue;
               }else {
                   mostRight.right = null;
                   printEdge(cur.left);
               }
           }
           cur = cur.right;
       }
       // 整个while结束之后
       printEdge(head);
   }
   
   // 逆序打印。
   public static void printEdge(Node node){
       Node tail =reverseEdge(node);
       Node cur = tail;
       while (cur != null ){
           System.out.println(cur.value);
           cur =cur.right;
       }
       // 打印完。再调整回去
       reverseEdge(tail);
   }

    // 单链表的反转。
   public static Node reverseEdge(Node node){
       Node pre = null;
       Node next = null;
       while (node != null){
           next = node.right;
           node.right = pre;
           pre = node;
           node = next;
       }
       return pre;
   }

复杂度分析

递归，迭代：
时间复杂度: 都是O(N)，要经过每一个节点
空间复杂度: 在二叉树退化成链表的时候最差是O(N)，平均状况是O(logn)

Morris遍历：
时间复杂度: 是O(N)
空间复杂度：O(1)

层序遍历

二叉树的深度优先遍历 ：先序遍历
二叉树的宽度优先遍历 ：队列。 -> 层序遍历。
102. 二叉树的层序遍历 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/*
要逐层打印
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

拓展：最大宽度 -> 还是可以用刚才的方法 
最大宽度在哪一层？-> 要维护一个层数的变量。
*/
public List<List<Integer>> levelOrder(TreeNode root){
    if (root == null) {
        return new ArrayList();
    }
    Queue<TreeNode> queue = new LinkedList();
    List<List<Integer>> res = new ArrayList();
    queue.add(root);
    while(!queue.isEmpty()){
        int count = queue.size();
        // 每一层都需要一个新的
        List<Integer> tmp = new ArrayList();
        // 只有当一层遍历完。才进入下一层。
        while(count > 0){
            root = queue.poll();
            tmp.add(root.val);
            if(root.left != null) {
                queue.add(root.left);
            }
            if(root.right != null) {
                queue.add(root.right);
            }
            count--;
        }
        res.add(tmp);
    }
    return res;
}

时间复杂度：O(N) 节点进出队列一次
空间复杂度：叶子节点层，需要存 N/2个节点。空间复杂度为O(N)

二叉搜索树

Binary search tree -> BST
若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树

验证BST

98. 验证二叉搜索树 - 力扣（LeetCode）
判断是否为BST: 中序遍历 -> 如果是升序的。就是BST

记录上一次 处理的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution{

    Long preVal = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if(root == null) {
            return true;
        }
        boolean left = isValidBST(root.left);
        if (!left){
            return false;
        }
        if(root.val > preVal){
            preVal = Long.valueOf(root.val);
        } else{
            return false;
        }
        return isValidBST(root.right);
    }
}

时间复杂度：O(N)
空间复杂度：O(N)

完全二叉树

Complete binary tree
若除最后一层外的其余层都是满的，并且最后一层要么是满的，要么在右边缺少连续若干节点，则此二叉树为完全二叉树

验证CBT

958. 二叉树的完全性检验 - 力扣（LeetCode）
基于层序遍历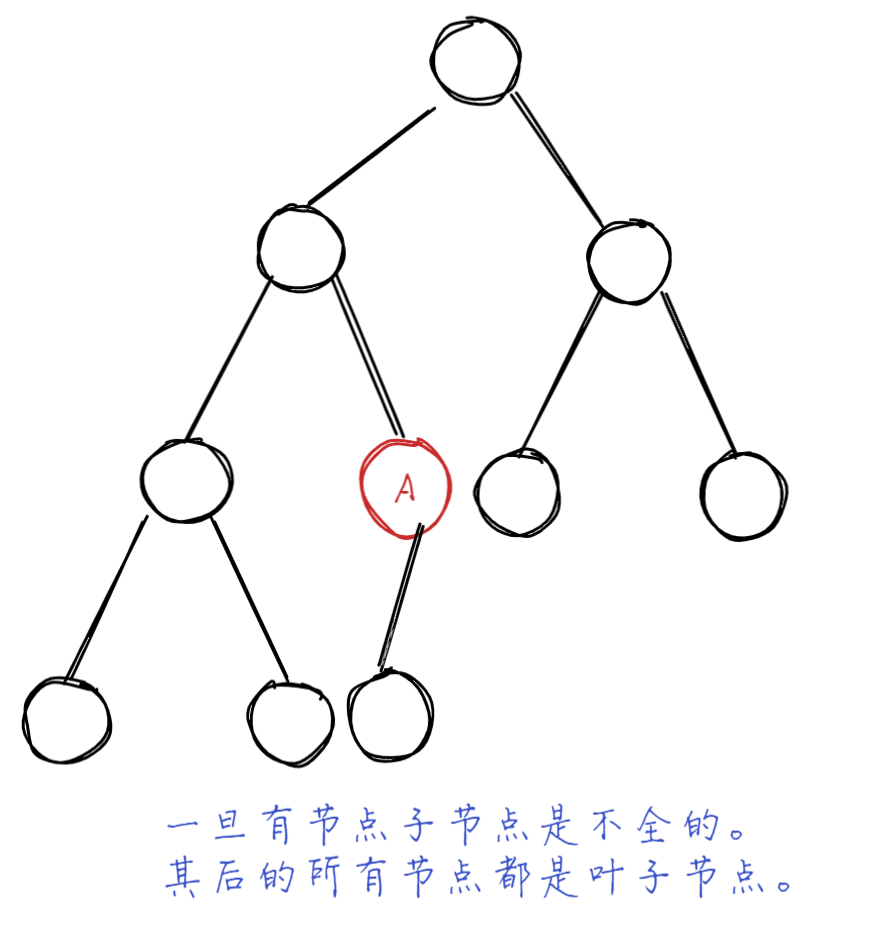

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution{

    public boolean isCBT(TreeNode root){
        if(root == null) {
            return true;
        }
        boolean isLeaf = false;
        TreeNode left = null;
        TreeNode right = null;

        Queue<TreeNode> queue = new LinkedList();
        queue.add(root);

        while(!queue.isEmpty()){

            root = queue.poll();

            // 就是为了减少代码量。要频繁用到
            left = root.left;
            right = root.right;

            // 判断false的两种情况。
            // 1. 左空右不空。2. 已经到达叶节点，叶节点却还有子节点
            if((left == null && right != null)) 
            || (isLeaf && (left != null || right != null)) 
            ){
                return false;
            }

            if(left != null){
                queue.add(left);
            }
            if(right != null){
                queue.add(right);
            }
            
            // 一旦遇到一个节点的存在节点不满的情况。当前节点一定是倒数第二层节点，
            // 其之后的节点全是叶节点
            if(left == null || right == null){
                isLeaf = true;
            }

        }
        // 整个遍历完。返回true;
        return true;
    }
}

满二叉树

Full Binary Tree( 或Perfect Binary Tree)

  • 所有internal node都有两个子节点；
  • 所有leaf node具有相同的level(或相同的height)。
  • 若一棵Full Binary Tree的leaf node之level为nn，整棵樹共有$2^n−1$個node。

另一种定义：二叉树的每个 节点恰好有 0 或 2 个子结点。

判断是否为满二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution{

    class Info{
        int height;
        int nodes;
        Info(int h, int n){
            this.height = h;
            this.nodes = n;
        }
    }

    public boolean isFullBinaryTree(TreeNode root){
        Info root = isFull(root);
        return root.nodes == (1 << root.height - 1);
    }

    public Info isFull(TreeNode root){
        if(root == null){
            return new Info(0, 0);
        }
        Info left = isFull(root.left);
        Info right = isFull(root.right);

        int height = Math.max(left.height, right.height) + 1;
        int nodes = left.nodes + right.nodes + 1;

        return new Info(height, nodes);
    }
}

平衡二叉树

对于任意的子树，其左右子树的高度差都<=1

判断是否为平衡树

剑指 Offer 55 - I. 二叉树的深度 - 力扣（LeetCode）
剑指 Offer 55 - II. 平衡二叉树 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
class Solution{

    class ReturnEntry{
        int height;
        boolean isBalanced;

        ReturnEntry(int height, boolean isBalanced){
            this.height = height;
            this.isBalanced = isBalanced;
        }
    }

    public boolean isBalanced(TreeNode root) {
        return isBalancedTree(root).isBalanced;
    }

    // 递归方法 -> 树形DP 如何把子树 信息传递。
    public ReturnEntry isBalancedTree(TreeNode root){
        if(root == null) {
            return new ReturnEntry(0, true);
        }
        ReturnEntry left = isBalancedTree(root.left);
        ReturnEntry right = isBalancedTree(root.right);

        height = Math.max(left.height, right.height) + 1;
        isBalanced = left.isBalanced && right.isBalanced
        && Math.abs(left.height - right.height) <= 1;
        
        return new ReturnEntry(height, isBalanced);
    }

    // 简化版
    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;
        int l = depth(root.left);
        int r = depth(root.right);
        return Math.abs(l - r)<=1 && isBalanced(root.left) && isBalanced(root.right);
    }

    // 二叉树深度的计算。
    int depth(TreeNode root){
        if(root == null) return 0;
        return Math.max(depth(root.left), depth(root.right)) + 1;
    }

    // 剪枝。如果左子树是不平衡的，就提前返回了。而计算深度是全部都要算一遍。
    public boolean isBalanced(TreeNode root) {
        // -1 表示非平衡
        return recur(root) != -1;
    }

    // 每次递归返回深度
    private int recur(TreeNode root) {
        if (root == null) return 0;
        int left = recur(root.left);
        if(left == -1) return -1;
        int right = recur(root.right);
        if(right == -1) return -1;
        return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
    }


}

复杂度：

  1. 先序遍历 + 深度。递归
    1. 时间复杂度 O(NlogN) 需要计算每一颗子树的深度。logN 层。 每层最多N节点。最少(N+1)/2
    2. 空间复杂度 O(N) 递归深度。退化成链表的情况。
  2. 后续遍历 + 剪枝
    1. 时间复杂度 O(N) 。减少了很多重复计算。最多遍历N个节点
    2. 空间复杂度 O(N)

最低公共祖先

236. 二叉树的最近公共祖先 - 力扣（LeetCode）

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

方法一 使用额外空间：

  1. 使用HashMap记录每个节点的父节点。
  2. 然后从n1往上遍历。加入一个set中。
  3. 然后从n2往上遍历。检查set中是否包含n2 往上的路径。

递归：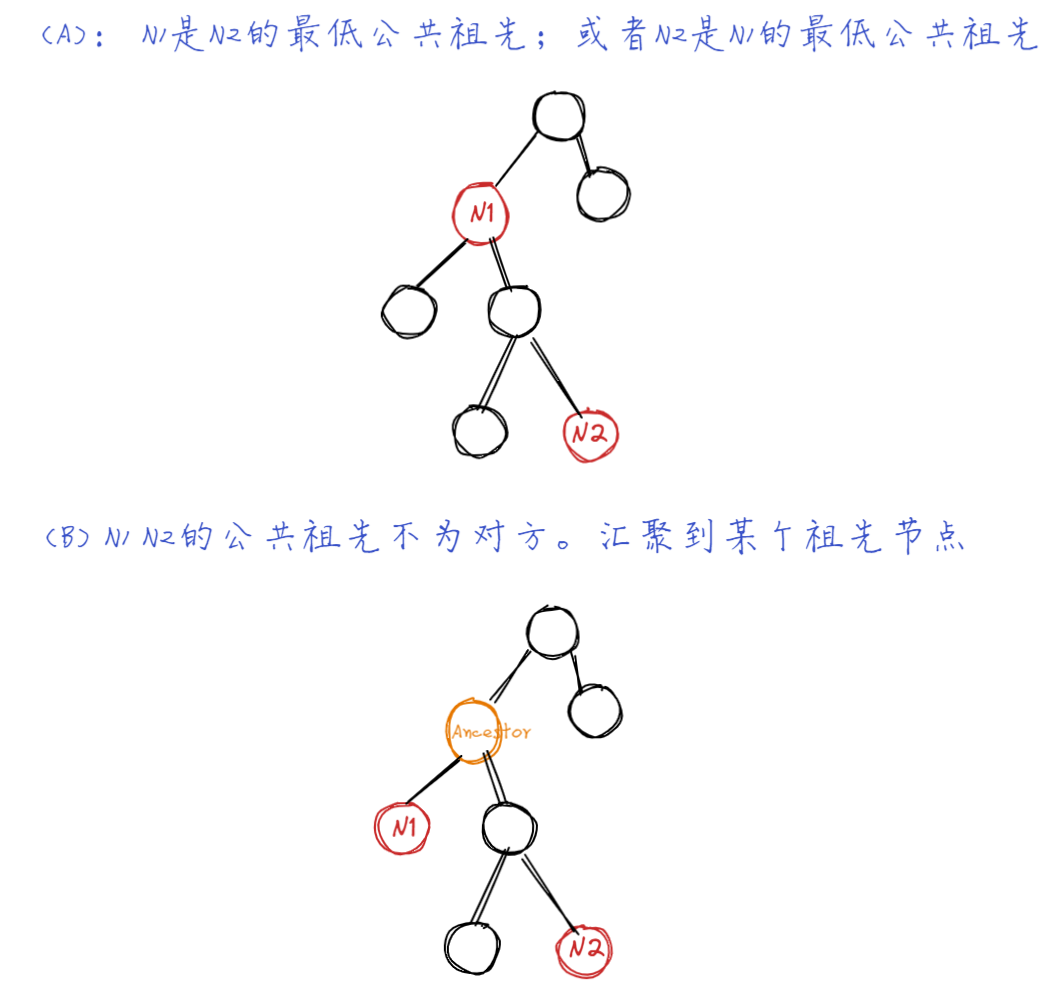
lca

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution{

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode n1, TreeNode n2){
        // 结束递归的条件
        // 只要当节点遇到n1 n2时才会向上返回值。否则都是返回空
        if(root == null || root == n1 || root == n2){
            return root;
        }

        TreeNode left = lowestCommonAncestor(root.left, n1, n2);
        TreeNode right = lowestCommonAncestor(root.right, n1, n2);

        // left, right都不为空。说明n1,n2分别在当前节点的左右子树上，当前节点为最低公共祖先
        if(left != null && right != null){
            return root;
        }

        // 有一个为空，返回非空的那个。两个都为空，则返回空。
        // 有一边为空。说明n1, n2在同一侧子树上。必然为 n1/n2 是 n2/n1的祖先的情况。
        return left != null ? left : right;

    }
}

查找后继节点

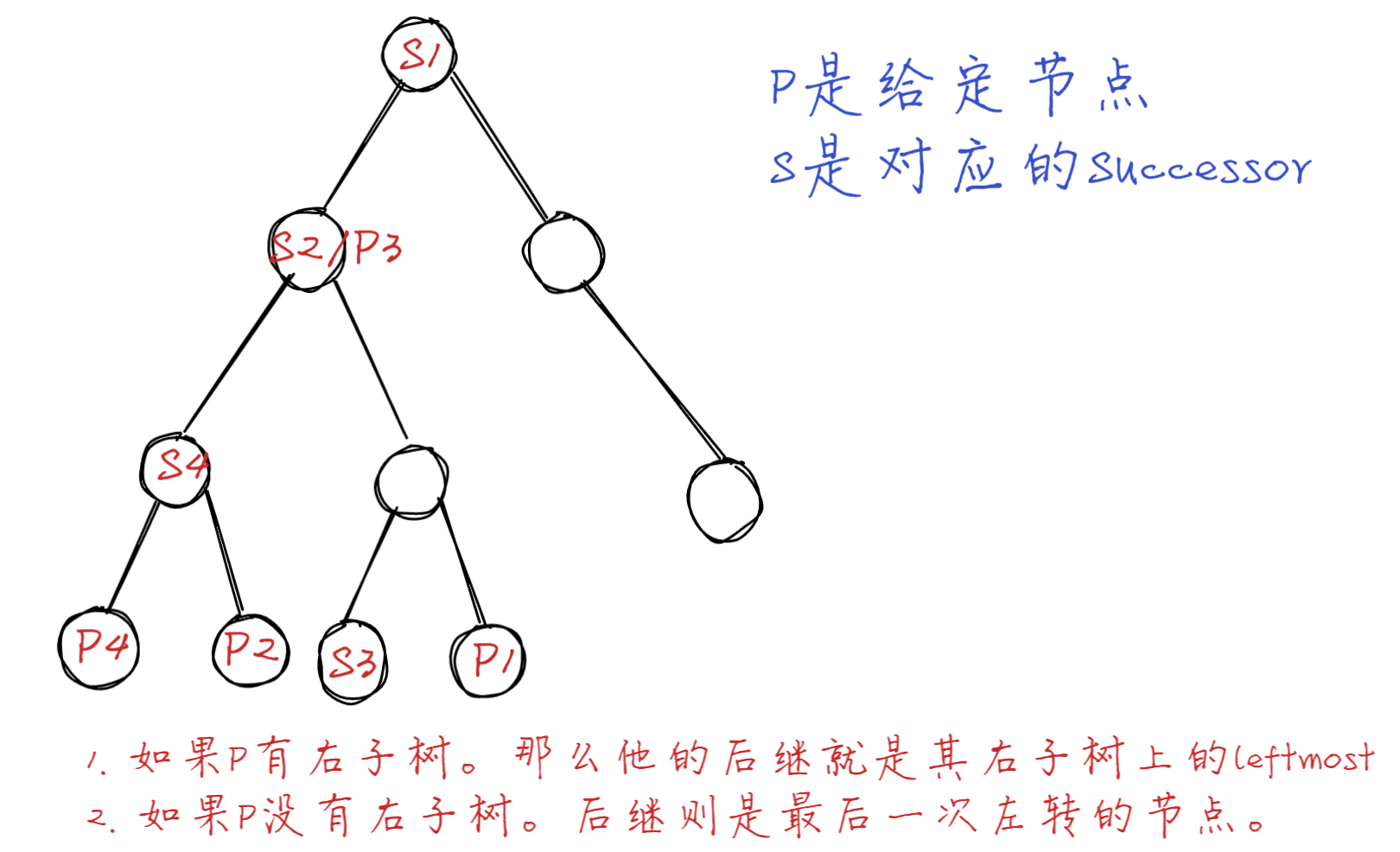
有父指针的二叉树

求一个二叉树中一个节点的后继节点（后继节点是中序遍历后的集合每个元素的下一个元素）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode parent;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

class Solution{
    public TreeNode inorderSuccessor(TreeNode root, TreeNode p){
        // 右子树不为空
        if(p.right != null) {
            TreeNode leftmost = p.right;
            while(leftmost.left != null) {
                leftmost = leftmost.left;
            }
            return leftmost;
        }

        // 右子树为空

        while(p.parent != null && p.parent.left != p){
            p = p.parent;
        }
        return p.parent;
    }
}

二叉搜索树

面试题 04.06. 后继者 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode inorderSuccessor(TreeNode p){
        // 使用一个cur指针 记录最后一次向左转的节点。即为没有右子树情况下的后继节点
        TreeNode cur = null;

        // 从根节点遍历找到p
        while(root.val != p.val){
            // 如果向右拐找到p cur不变。
            if(p.val > root.val){
                root = root.right;
            // 如果过程中向左拐了，要更新cur
            } else{
                cur = root;
                root = root.left;
            }
        }

        // 循环结束时。root指向p
        // 如果右子树存在。则找出右子树上的leftmost。没有右子树。则返回cur
        if(root.right == null){
            return cur;
        } else{
            // 找到右子树的leftmost
            root = root.right;
            while(root.left != null){
                root = root.left;
            }
            return root;
        }
    }
}

这两题的区别在于：

  • 二叉搜索树能通过val从root找到p
  • 普通二叉树则需要通过parent指针来向上溯源。

序列化和反序列化

297. 二叉树的序列化与反序列化 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {
    //先序遍历
    public String serialize(TreeNode root){
        if(root == null){
            return "#_";
        }
        StringBuilder data = new StringBuilder(root.val + "_");
        String left = serialize(root.left);
        String right = serialize(root.right);
        data.append(left).append(right);
        return data.toString();
    }

    public TreeNode deserialize(String data){
        String[] arr = data.split("_");
        Queue<Integer> queue = new LinkedList();
        for(int i = 0; i < arr.length; i++){
            if("#".equals(arr[i])){
                queue.add(null);
            } else{
                queue.add(Integer.valueOf(arr[i]));
            }
        }
        return reconTree(queue);
    }

    public TreeNode reconTree(Queue<Integer> data) {
        Integer val = data.poll();
        if(val == null) {
            return null;
        }
        TreeNode root = new TreeNode(val);
        root.left = reconTree(data);
        root.right = reconTree(data);
        return root;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));

复杂度：

  • 时间复杂度：O(N)
  • 空间复杂度：O(N)

折纸问题

纸条对折。 从纸条的上方按顺序打印折痕方向


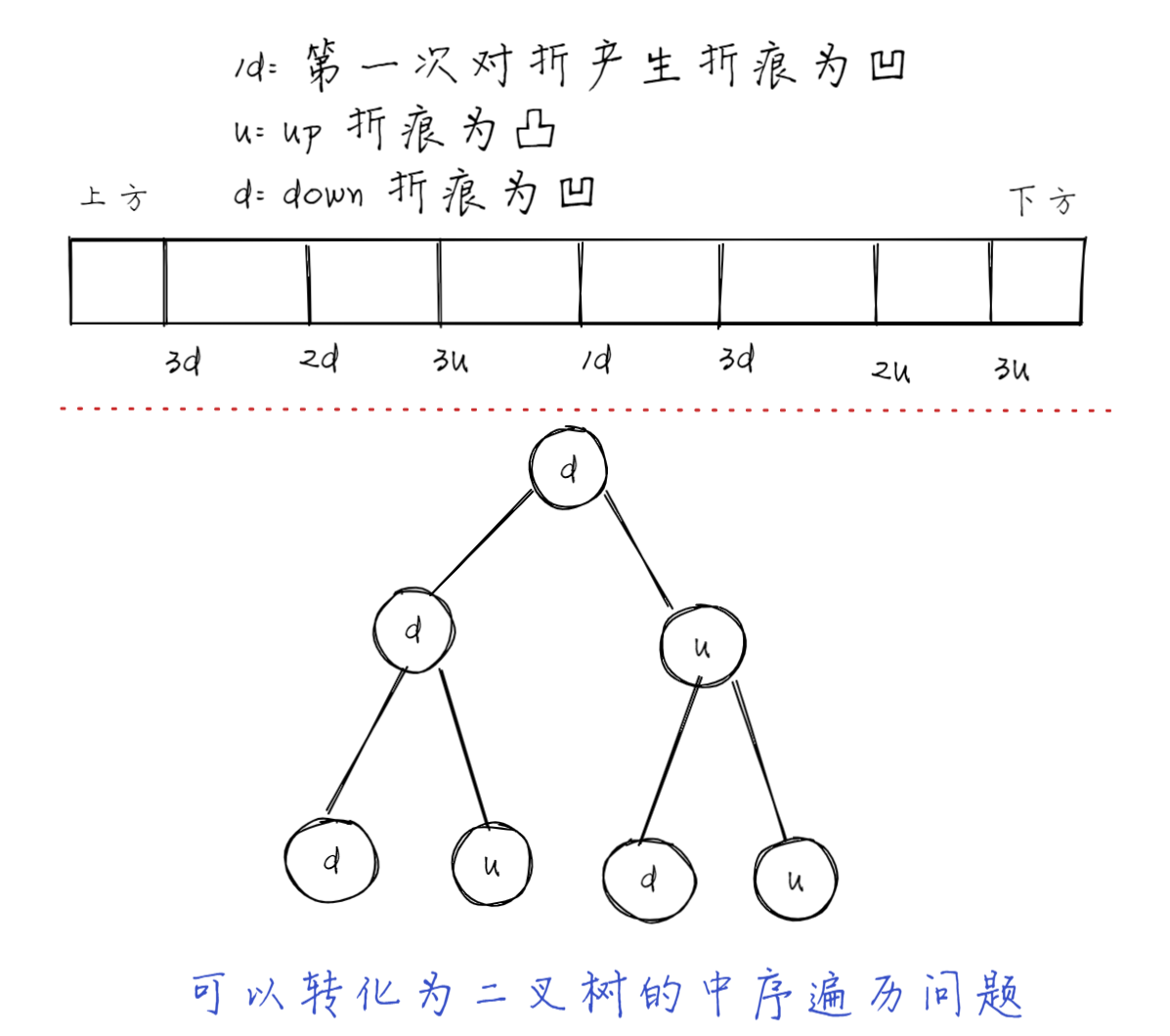
左子树都是凹，右子树都是凸

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution{

    public printFoldLine(int n){
        // 根节点为对折一次产生的凹折痕
        print(n, 1, true);
    }

    // n表示对折次数。i为当前对折的次数。down表示折痕为凹
    public void print(int n, int i, boolean down){
        if(i > n) {
            return;
        }
        print(n, i + 1, true);

        System.out.println(down ? "down" : "up");

        print(n, i + 1, false);
    }
}