LeetCode Weekly Contest 301

Notes

Q1

6112. 装满杯子需要的最短总时长 - 力扣（LeetCode）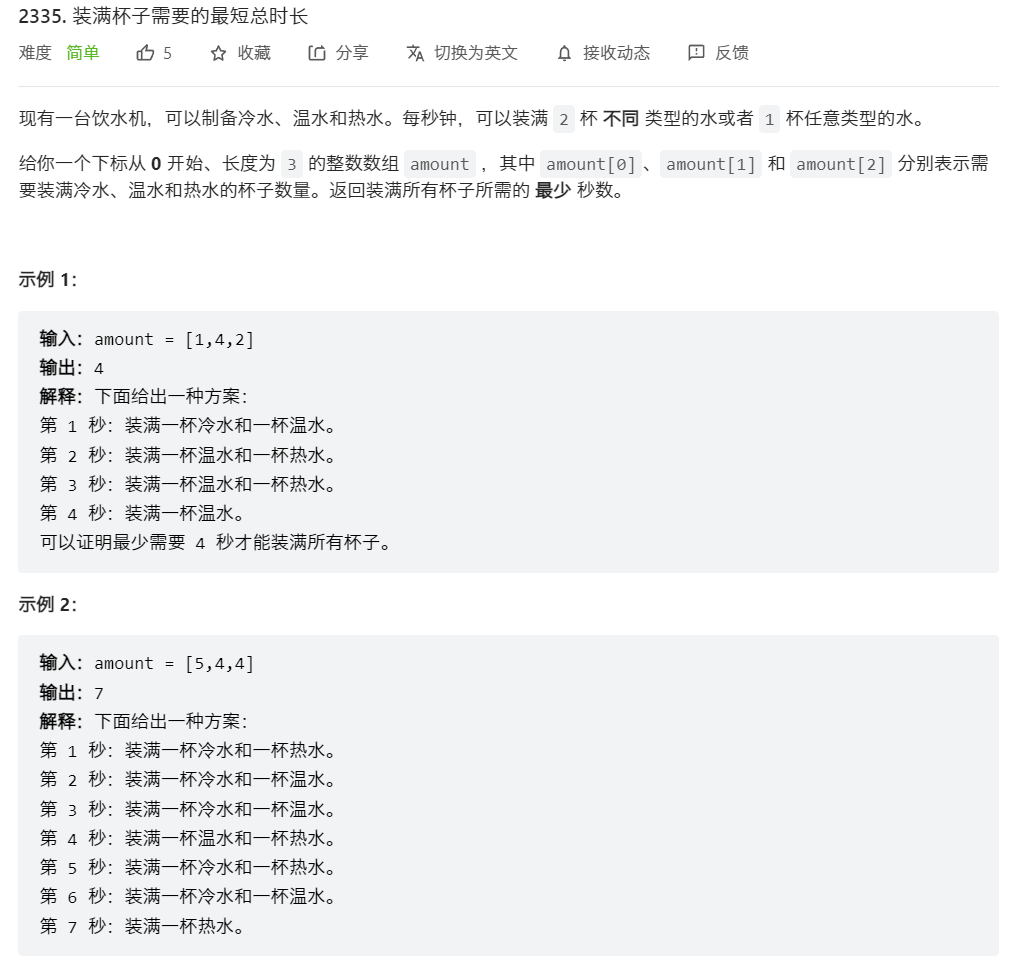

提交

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int fillCups(int[] amount) {
        Arrays.sort(amount);
        int min = amount[0];
        int mid = amount[1];
        int max = amount[2];
        int res = 0;
        res += min;
        // 先把max 减到和mid一样
        while(min >0 && max > mid){
            max--;
            min--;
        }
        // 然后再同时减
        max -= min/2;
        mid -= (min + 1)/2;
        res += Math.max(max, mid);
        return res;
    }
}

贪心

从最大的两个数开始减少

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int fillCups(int[] amount) {
        int res = 0;
        while(true){
        // 每次都排序。从最大的两个数开始减。如果中间的数都为0。再加上残余的最大值。
            Arrays.sort(amount);
            if (amount[1] == 0) break;
            amount[2]--;
            amount[1]--;
            res++;
        }
        return res + amount[2];
    }
}

公式

如果 最大值 大于另外两个和。返回最大值
如果 最大值小于另外两个和。
a >= b >= c
当 a <= b +c的时候，每次必然可以拿两个数。
当a - 1, b-1, c 最大值仍然为a时， 还是满足a <= b +c这个性质。每次都可以从两边拿
当最大值变为c的时候，c同样可以和a一样操作

1
2
3
4
5
6
7
class Solution {
    public int fillCups(int[] a) {
        Arrays.sort(a);
        if(a[2] >= a[0] + a[1]) return a[2];
        else return (a[0] + a[1] + a[2] + 1) /2;
    }
}

Q2

6113. 无限集中的最小数字 - 力扣（LeetCode）

提交

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class SmallestInfiniteSet {
    int[] s = new int[1000];

    public SmallestInfiniteSet() {
        for(int i = 0; i < 1000; i++){
            s[i] = i + 1;
        }
    }
    
    public int popSmallest() {
        int res = 0;
        for(int i = 0; i < 1000; i++){
            if(s[i] != -1) {
                res = s[i];
                s[i] = -1;
                break;
            }
        }
        return res;

    }
    
    public void addBack(int num) {
        if(s[num-1] == -1){
            s[num - 1] = num;
        }
    }
}

/**
 * Your SmallestInfiniteSet object will be instantiated and called as such:
 * SmallestInfiniteSet obj = new SmallestInfiniteSet();
 * int param_1 = obj.popSmallest();
 * obj.addBack(num);
 */

set

使用set存被删除的数。无限集如果数据量大的话，就过不了了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class SmallestInfiniteSet {
    HashSet<Integer> set;
    public SmallestInfiniteSet() {
        set=new HashSet<>();
    }
    
    public int popSmallest() {
        int res=1;
        while(set.contains(res)){
            res++;
        }
        set.add(res);
        return res;
    }
    
    public void addBack(int num) {
        if(set.contains(num)) set.remove(num);
    }
}

Q3

6114. 移动片段得到字符串 - 力扣（LeetCode）
同 777. 在LR字符串中交换相邻字符 - 力扣（LeetCode）

提交

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public boolean canChange(String start, String target) {
        int n = start.length();
        // L不能超过L的原始位置。只能往左。R也是同理。
        if(!start.replace("_", "").equals(target.replace("_", ""))) return false;
        
        
        int t = 0;
        for (int i = 0; i < n; i++)
            if (start.charAt(i) == 'L') {
                while (target.charAt(t) != 'L') t++;
                if (i < t++) return false;
            }

        t = 0;
        for (int i = 0; i < n;i++)
            if (start.charAt(i) == 'R') {
            // 如果i 不大于t t移动到下一个位置。继续寻找下一个L R
                while (target.charAt(t) != 'R') t++;
                if (i > t++) return false;
            }


        return true;
    }
}

双指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    bool canChange(string start, string target) {
        int n = start.size();
        for(int i = 0,j = 0;i < n;)
        {
            while(i < n && start[i] == '_')i++;
            while(j < n && target[j] == '_')j++;
            // 如果分别为L R 显然相对位置不同。返回false
            if(start[i] != target[j])return false;
            // target的L要在更左。R要在更右。
            if(start[i] == 'R' && j < i)return false;
            if(start[i] == 'L' && j > i)return false;
            i++;
            j++;
        }
        return true;
    }
};

Q4

6115. 统计理想数组的数目 - 力扣（LeetCode）

组合数 DP

n是数组的长度，t是不同元素的个数。
如果可以相同，就是计算组合数从n -1个位置里 选出t-1个位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
    const int MOD = 1000000007;
    const int MAXP = 16; // 2^16 > 10000, n <= 10000

public:
    int idealArrays(int n, int K) {
        // nlnn 求因数
        vector<vector<int>> fac(K + 1);
        for (int i = 1; i <= K; i++) 
            // 求的是j的因数的数组
            for (int j = i << 1; j <= K; j += i) 
            fac[j].push_back(i);

        // 计算子问题的答案
        vector<vector<long long>> f;        
        f.resize(K + 1, vector<long long>(20));
        // i的最大值为K
        for (int i = 1; i <= K; i++) {
            // 以1为结尾只有一种方案
            f[i][1] = 1;
            for (int j = 2; j <= MAXP; j++) 
            // t是i的因数。加上子问题的方案书。以因数为结尾。长度减去1的情况
                for (int t : fac[i]) 
                f[i][j] = (f[i][j] + f[t][j - 1]) % MOD;
        }

        // 求组合数
        vector<vector<long long>> C;
        C.resize(n + 1, vector<long long>(20));
        C[0][0] = C[1][0] = C[1][1] = 1;
        for (int i = 2; i <= n; i++) {
            C[i][0] = 1;
            for (int j = 1; j <= i && j <= MAXP; j++) 
                C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % MOD;
        }

        // 统计最终答案
        long long ans = 0;
        for (int i = 1; i <= K; i++) 
            for (int j = 1; j <= MAXP; j++) 
        // 以i为最后一个元素。且数组长度为j的数量。组合数-> 计算出元素重复使用的情况
            ans = (ans + C[n - 1][j - 1] * f[i][j]) % MOD;
        return ans;
    }
};

暴力搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    int n, m;
    int ans = 0;
    const int MOD = 1e9 + 7;
    vector<vector<int>> f;

    void dfs(int u, int cnt) {
        ans = (ans + f[n - 1][cnt - 1]) % MOD;
        // 数组长度小于n
        if (cnt < n) {
            // 从起点开始 乘以所有的质因数，小于最大值
            for (int i = 2; i * u <= m; i ++ )
                dfs(i * u, cnt + 1);
        }
    }

    int idealArrays(int n, int m) {
        this->n = n, this->m = m;
        f = vector<vector<int>>(n, vector<int>(20));
        for (int i = 0; i < n; i ++ )
            for (int j = 0; j < 20 && j <= i; j ++ )
                // j为0
                if (!j) f[i][j] = 1;
                // 组合数
                else f[i][j] = (f[i - 1][j] + f[i - 1][j - 1]) % MOD;

        for (int i = 1; i <= m; i ++ )
            // 从1开始搜索 到最大值为止。
            dfs(i, 1);

        return ans;
    }
};